
Spirála je křivka, která obíhá pevně daný ústřední bod a přitom se od tohoto bodu soustavně vzdaluje. Formální matematická rovnice (definice), která by zahrnovala všechny spirály, jako je tomu u kuželoseček, neexistuje.
Mezi nejznámější spirály patří:
- Archimédova spirála,
- Fermetova spirála (spirálu navrhl Fermat v roce 1636),
- Hyperbolická spirála (spirálu objevil Piere Varignon v roce 1704),
- Lituus (spirálu navrhl Cotes v roce 1722),
- Logaritmická spirála (první, kdo se jí začal zabývat, byl René Descartes přibližně v roce 1638),
- Klotoida (Eulerova nebo Cornuova spirála).
S ohledem na praktické využití se zaměříme na Archimédovu spirálu.
Matematické vyjádření Archimédovy spirály
Archimédova spirála, kterou před 2300 lety popsal Archimédes, je rovinná křivka (spirála), jejíž poloměr roste lineárně s velikosti úhlu. Tuto spirálu lze popsat jako trajektorii bodu, který se rovnoměrně posunuje po polopřímce od jejího počátku v bodě O, zatímco polopřímka se kolem bodu O rovnoměrně otáčí. Pól spirály a počátek spirály jsou u Archimédovy spirály totožné. Paprsek vycházející z pólu spirály protíná spirálu v bodech, jejichž vzdálenosti od pólu tvoří aritmetickou posloupnost.
Rovnice Archimédovy spirály má tvar r = a · ϕ, kde:
- a … je kladné číslo,
- ϕ … je úhel polopřímek, který svírají s polární osou.
Délka spirála se určuje podle parametrické rovnice.

S ohledem na praktickou konstrukci v SOLIDWORKSu prostřednictvím zadávaných parametrů, se těmito rovnice nebudeme dále zabývat.
Archimédova spirála v SOLIDWORKSu
V praxi se se spirálou můžete setkat při konstrukci hodinek (spirálové pérko) nebo pokud studujete strojírenský obor, tak jste se již setkali s Archimédovou spirálou u soustružení, kde soustružnický nůž při příčném posuvu vstupuje do obrobku ve směru kolmém na osu obrobku a trajektorie má tvar zmiňované křivky.
S Archimédovou spirálou se setkáte i při tzv. podsoustružování, které se využívá pro obrábění hřbetních ploch obráběcích nástrojů (hřbetní plocha tvarové frézy, tvarového kotoučového nože, závitníků větších průměrů atd.). Výroba takových nástrojů se provádí na speciálních podsoustružovacích soustruzích. Princip výroby je zřetelný z obrázku níže.



Jak zkonstruovat Archimédovu spirálu
Spirálu v SOLIDWORKSu vytvoříte prostřednictvím prvku Šroubovice/spirála (CommandManager Prvky → Křivky → Šroubovice/spirála),…
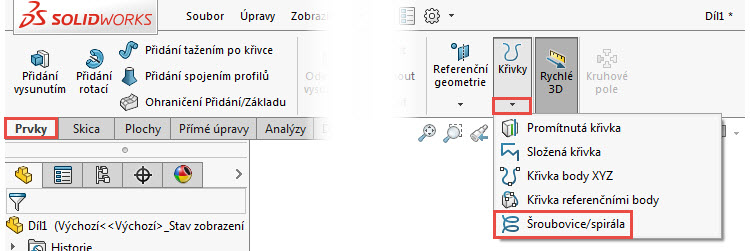
… kde v PropertyManageru Šroubovice/spirála vyberte v poli Určená z roletové nabídky Spirála.
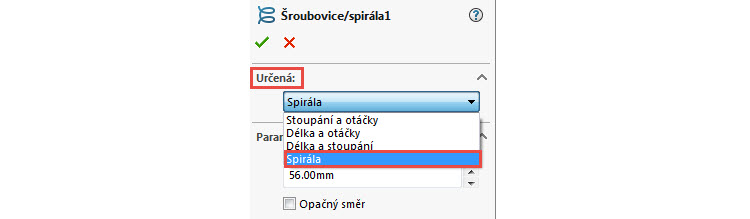
Parametry spirály jsou:
- Stoupání,
- volba opačného směru (Opačný směr) vůči zvolené rovině,
- Otáčení,
- Počáteční úhel,
- možnost otáčení Doprava (výchozí) nebo Doleva.
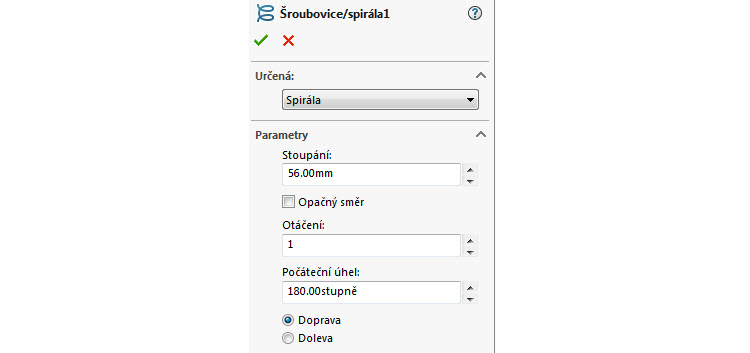
V grafickém náhledu můžete sledovat formování spirály podle nastavených parametrů, jako je tomu u jiných příkazů. Spirálu dokončíte potvrzovacím tlačítkem.

Zadání (samostatné cvičení)
Zkonstruujte tvar Archimédovy spirály, která tvoří část trasy pro modelování ztekucovací spirály na med, znáte-li tyto hodnoty:
- vnější průměr 300 mm (v Horní rovině),
- stoupání 30 mm,
- počet otáček…4,5,
- počáteční úhel 270°,
- směr otáčení…vlevo.
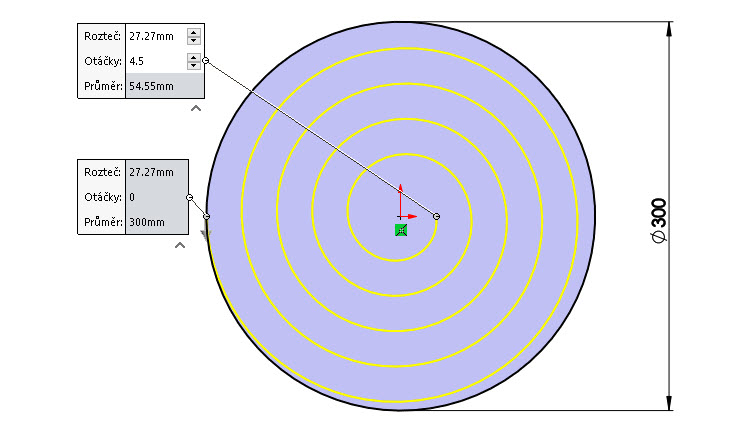
Pokud budete chtít vymodelovat celou ztekucovací spirálu, podívejte se na její rozměry (rozměry níže) a pokračujte.

Tip: Nebudete-li si vědět rady, podívejte na návod krok za krokem (připravujeme).






Komentáře k článku (0)
Přidávat komentáře k článku mohou pouze přihlášení uživatelé.
Chcete-li okomentovat tento článek, přihlaste se nebo se zaregistrujte.