Postup modelování kuželového kola s přímými zuby (parametricky) #1

Kuželová soukolí slouží k přenosu krouticího momentu mezi dvěma hřídeli s různoběžnými osami a vyrábí se s přímým a šikmým ozubením. V tomto návodu si ukážeme pokročilý postup modelování, ve kterém použijeme rovnice, globální proměnné a parametrizaci pro konstrukci kuželová kola s přímými zuby.

V tomto návodu si ukážeme postup krok za krokem, jak zkonstruovat kuželové kolo parametricky tak, aby se při změně počtu zubů a modulu (výchozí podmínky pro definici kuželového kola) automaticky přepočítaly všechny rozměry a upravil celý model kola.

Upozornění: Při určitých hodnotách model může přepočet a konstrukce selhat a to v případě, že patní kružnice bude větší než základní. V takových případech je nutno upravit patřičné skici a přistupovat k úpravám velmi zodpovědně a promítnutou zubovou mezeru a entity ořezat do požadovaného tvaru tak, aby byl model kuželového kola korektní.

Postup modelování kuželového kola:

• Díl 1. – Rovnice a výpočty
• Díl 2. – Konstrukce profilu kuželového kola (připravujeme)
• Díl 3. – Konstrukce kružnic (připravujeme)
• Díl 4. – Konstrukce zubové mezery (připravujeme)
• Díl 5. – Odebrání zubové mezery, zaoblení paty zubu, kruhové pole (připravujeme)

Postup modelování kuželového kola s přímými zuby

Založení nového dílu, uložení dokumentu

Založte si nový díl.

Uložte dokument do složky C:\Mujsolidworks.cz\kuzelova kola (1) pod názvem (například) 20180326-01.SLDPRT (2). Do pole Popis uveďte název součásti KUŽELOVÉ KOLO. Dokončete uložení tlačítkem Uložit (3).

V první části návodu se zaměříme na zadání rovnic, globálních proměnných a konstrukci skici s rozměry, které použijeme pro konstrukci zubové mezery.

Rovnice

S ohledem na tvorbu kuželového ozubeného kola s přímými zuby v parametrickém pojetí si nejdříve definujeme potřebné rovnice do tabulky Rovnice. Ze záložky Nástroje vyberte Rovnice.

Tabulka Rovnice obsahuje několik sloupců pro definici názvu, hodnoty/rovnice, výsledku (počítá se automaticky) a poznámky.

Zadejte postupně podle obrázku všechny globální proměnné, které budeme v rámci názorného postupu krok za krokem potřebovat k tomu, abychom parametricky vymodelovali kuželového ozubené kolo:

• modul vnější čelní – “m_et“ = 2,
• počet zubů pastorku – “z1“ = 20,
• počet zubů kola – “z2“ = 30,
• korekce pastorku – “X1“ = 0,
• korekce kola – “X2“ =0,
• úhel os – “sigma“ =90stupně,
• šířka věnce – “b“ = 10,
• úhel záběru čelní – “alpha_t“ = 20stupně,
• jednotková výška hlavy zubu – “ha“ = 1,
• jednotková hlavová vůle – “c“ = 0.2,
• jednotkové zaoblení – “rf“ = 0.3,
• převodový poměr – “u“ = “z2“ / “z1“.

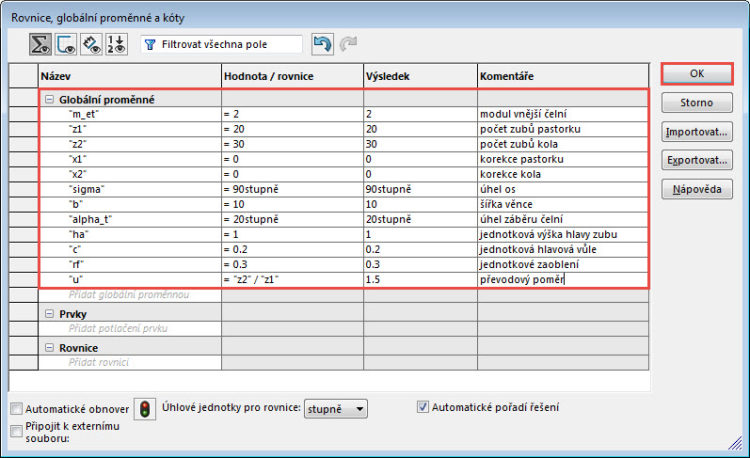
Zadávání globálních proměnných dokončete tlačítkem OK.

Globální proměnné můžete zkontrolovat ve složce Rovnice ve FeatureManageru.

Vyberte rovinu Horní a z kontextového panelu nástrojů vyberte příkaz Načrtnout skicu. První skica, kterou v modelu dílu vytvoříte, se automaticky orientuje do pohledu kolmého na rovinu skici.

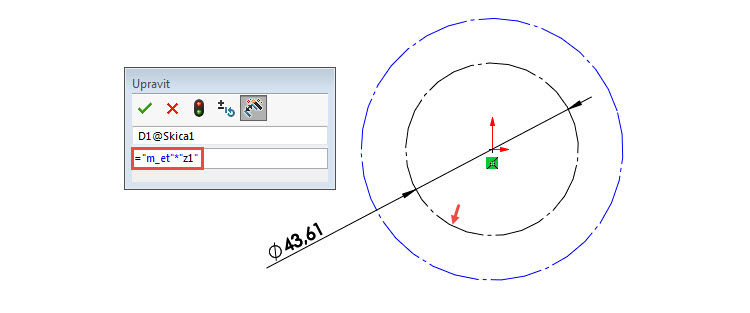
Klávesou S si zobrazte panel zkratek a vyberte příkaz Kružnice. Nakreslete dvě kružnice se středy v počátku souřadného systému.

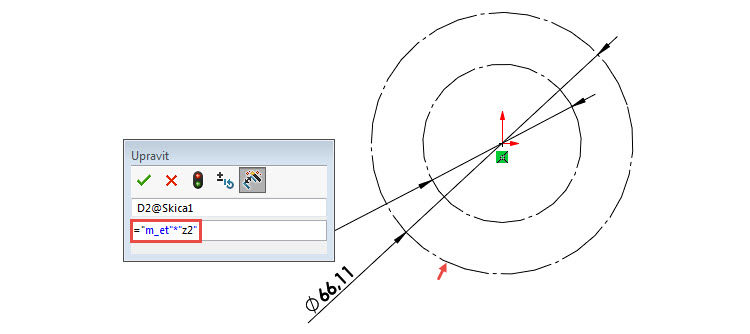
Horním gestem vyberte příkaz Inteligentní kóta a zakótujte průměr jedné z kružnice. Do pole Upravit zadejte hodnotu v podobě rovnice =“m_et“*“z1″. Dokončete kótování potvrzovacím tlačítkem.

Zakótujte druhou kružnici pomocí rovnice =“m_et“*“z2″.

Klávesou S si zobrazte Panel zkratek a vyberte příkaz Osa a nakreslete tři osy, jejichž počátky vycházejí z počátku souřadného systému. Vycházejte z grafického znázornění na obrázku. Pouze jedna z os je dána vazbou Vodorovná.

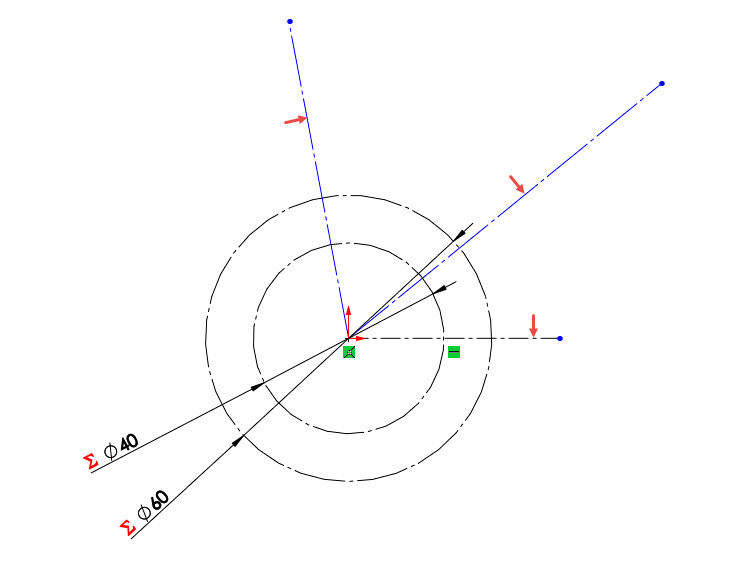
Uložte dokument (Ctrl + S).

Zakótujte úhel mezi vodorovnou a šikmou osou a pro zadání hodnoty použijte globální proměnnou sigma. Zadání proměnné do pole Upravit proveďte tak, že napíšete rovnítko a následně vyberte proměnnou z nabídky.

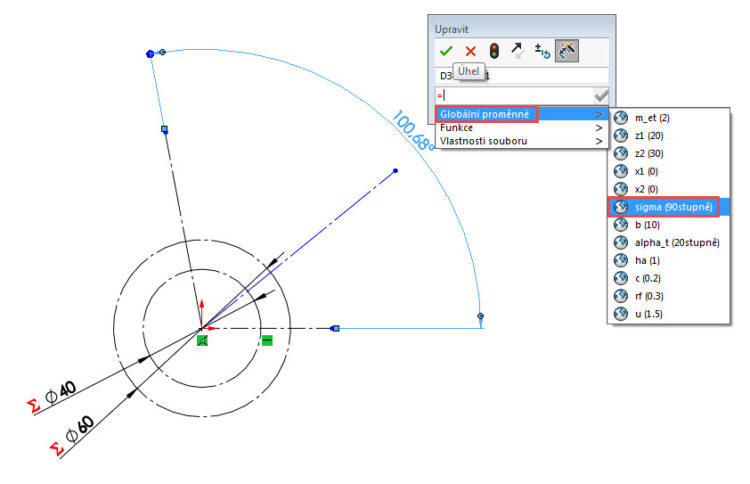
V poli Upravit upravte název kóty → sigma@Skica1.

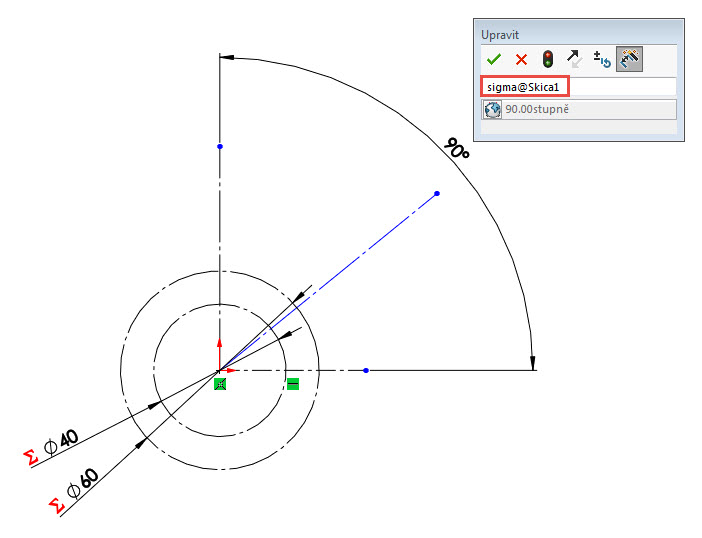
Postupujte v kótování dalšího úhlu, jehož hodnotu zadejte prostřednictvím rovnice =atn(sin( „sigma“)/(„u“+cos( „sigma“))).

V poli Upravit přejmenujte název kóty → delta_1@Skica1.

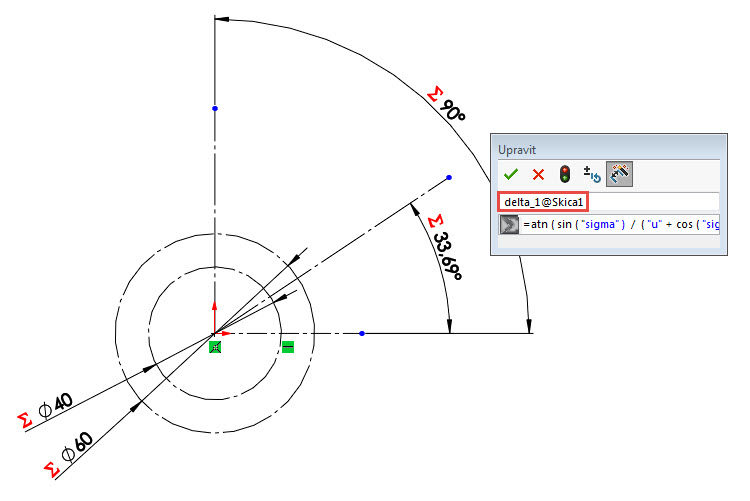
Zakótujte doplňkový úhel a kótu vytvořte jako řízenou. V poli Hlavní hodnota změňte název kóty → delta_2@Skica1.

Zakótujte délku vodorovné osy =“z1″/cos( „delta_1@vypocty“) a změňte její název → zv1@Skica1.

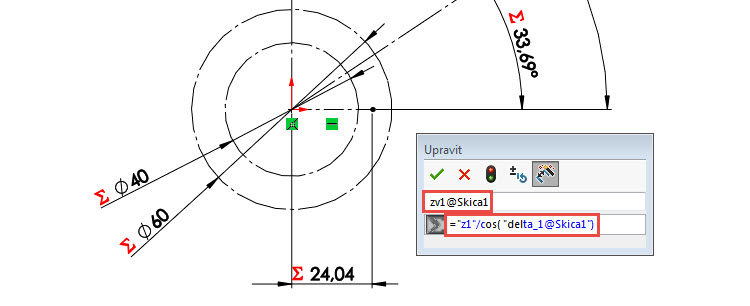
Zakótujte délku svislé osy =“z2″/cos( „delta_2@Skica1“) a změňte její název → zv2@Skica1.

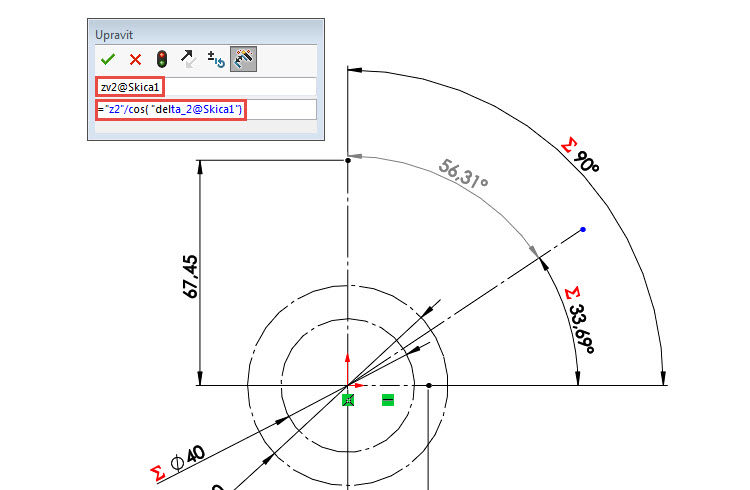
Uložte dokument (Ctrl + S).

Nakreslete dvě kružnice, jejichž středy leží v pravém koncovém bodě vodorovné osy.

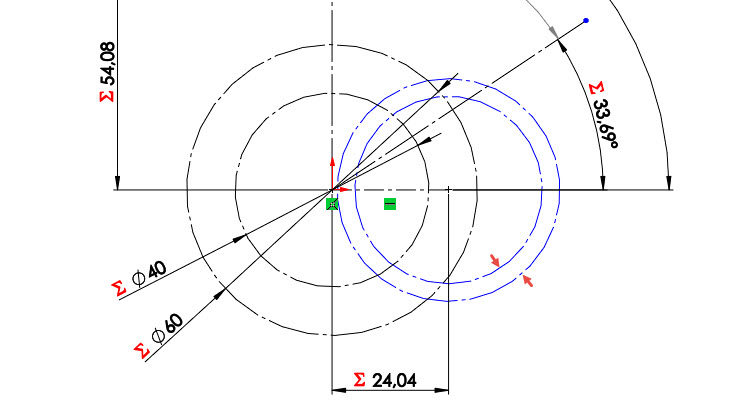
Zakótujte rozměr první kružnice rovnicí =“m_et“ * „zv1@Skica1“ a změňte její název → dve1@Skica1.

Zakótujte rozměr druhé kružnice rovnicí =“dve1@Skica1″ * cos ( „alpha_t“ ) a změňte její název → dveb1@Skica1.

Nakreslete dvě kružnice, jejichž středy leží v horním koncovém bodě svislé osy.

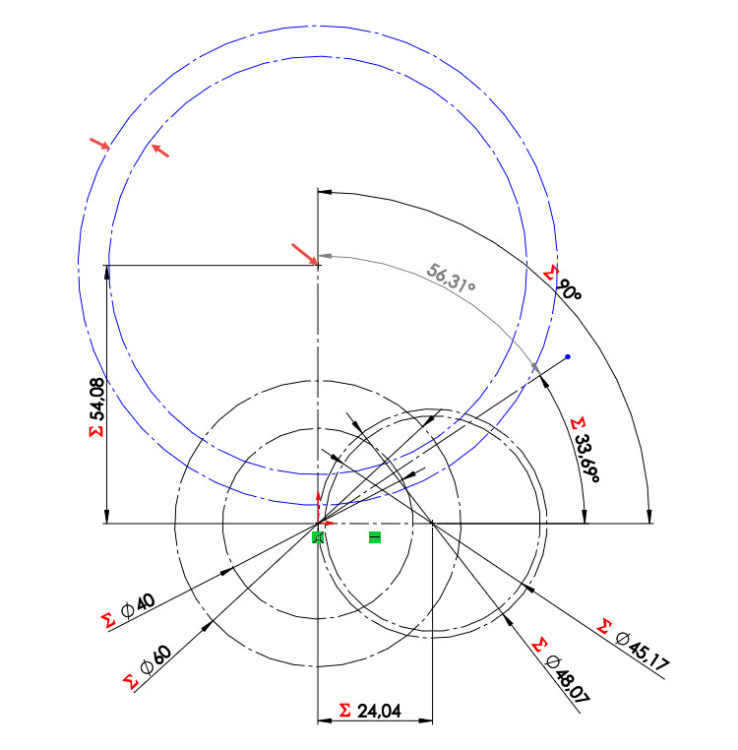
Zakótujte rozměr první kružnice rovnicí =“m_et“*“zv2@Skica1″ a změňte její název → dve2@Skica1.

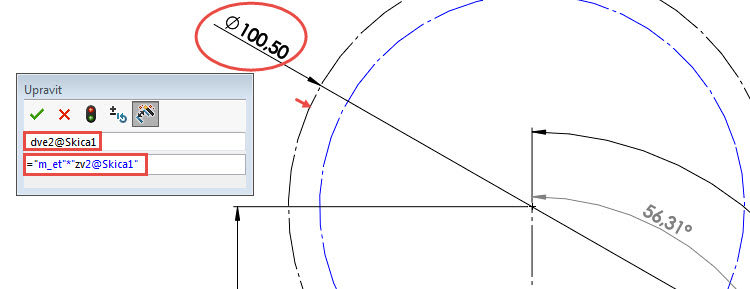
Zakótujte rozměr druhé kružnice rovnicí =“dve2@Skica1″ * cos ( „alpha_t“ ) a změňte její název → dveb2@Skica1.

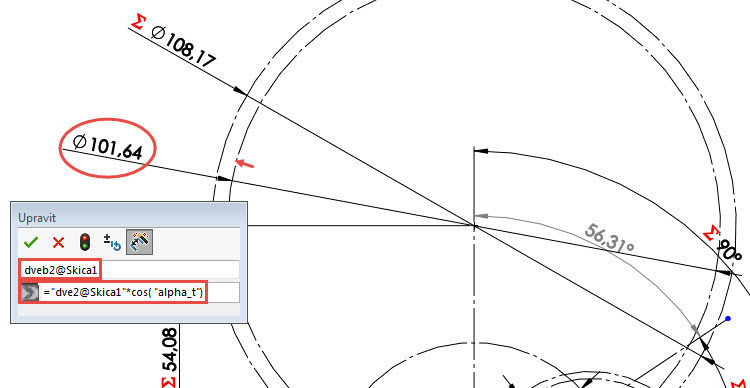
Konstrukce pro definici a použití rozměrů k dalším výpočtům je hotová.

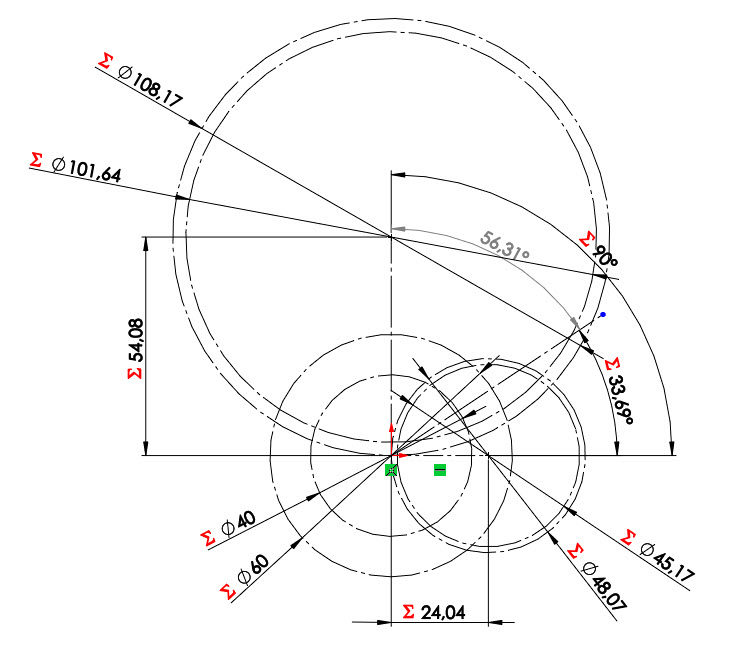
Ukončete skicu a uložte dokument (Ctrl + S).

Pokračujte v konstrukci kuželového kola podle druhého dílu návodu.